LLMForEverybody
0基础学习AI大模型必备数学知识之线性代数(二)矩阵行规约,秩和行阶矩阵
1. 系列介绍
AI是理科+工科的交叉学科,牢固的数学知识有助于理解算法的本质。
线性代数是AI领域的基础数学知识之一,掌握线性代数知识对于理解深度学习算法和模型至关重要。本系列将介绍AI大模型必备的线性代数知识,帮助大家更好地理解AI大模型的原理和应用。
我们会着重介绍各种基础概念,关键数学名词会加注英文以求更好的理解。我们也会分享一些大学里老师不会教的小知识,目的是帮助大家建立起对线性代数的直觉式认识。
2. 矩阵行规约 Matrix Row Reduction
2.1 二元一次方程组
在学习初等代数的时候,我们会从二元一次方程组开始,逐渐引入三元一次方程组,四元一次方程组,直到n元一次方程组。
在高等代数/线性代数里,矩阵的行规约指的是在对方程组用消元法求解时,对应的系数矩阵的行变换。
2.2 行变换
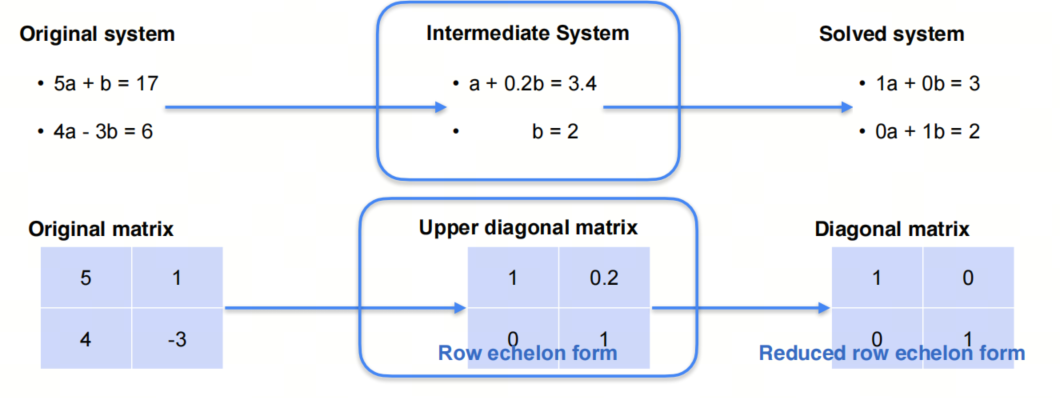
上图中我们在解一个二元一次方程组,注意对应的系数矩阵的行变换。
这边出现了两个新术语:
- Row echelon form 行阶梯形式(行阶梯形矩阵)
- Reduced row echelon form 行最简梯形
- echelon是法语,意思是梯形,这个概念在数学中很常见,比如梯形数列,梯形函数等。
3. 秩 Rank of a Matrix
3.1 保持奇异性的矩阵行操作
- 如果你不清楚什么是奇异性,可以参考前文。简单来讲,奇异矩阵指的是行列式为0的矩阵。
- 交换行
- 乘以一个非零常数
- 加上另一行的倍数
3.2 秩 Rank
我们还是用一组句子来类比:

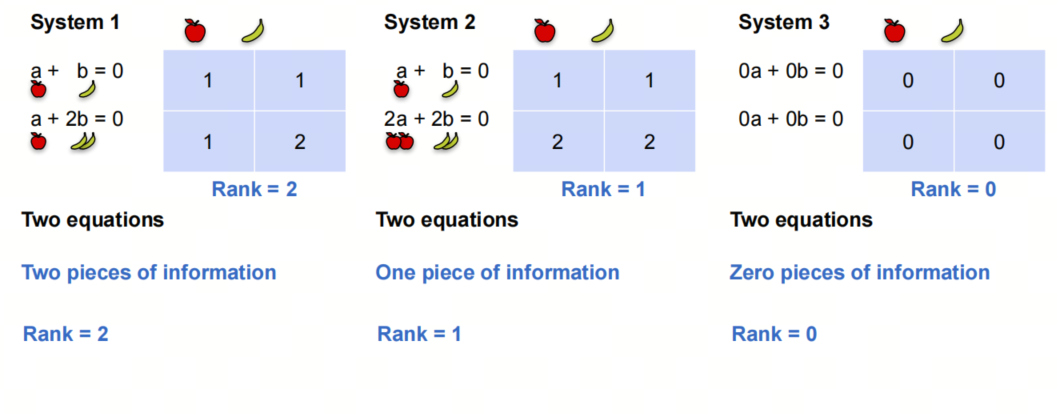
上图中,第一个系统包含两个句子,第二个系统包含两个重复句子,第三个系统包含两个句子,但没有任何信息量。
我们说第一个系统的rank是2,第二个系统的rank是1,第三个系统的rank是0。
3.3 秩和系统解的关系
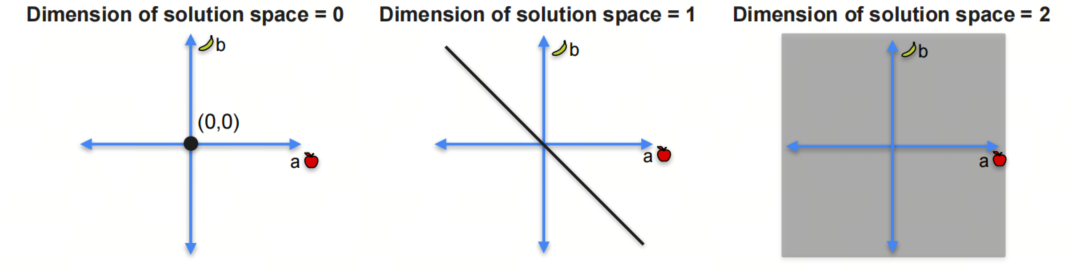
对于上述的三个系统,我们可以看出,rank=2的系统有唯一解;rank=1的系统有无穷多解,但在一条线上;rank=0的系统有无穷多解,且在平面上。
如下图所示:
4. 行阶(梯形)矩阵 Row Echelon Form
行阶梯形矩阵是指矩阵的第一个非零元素为1,且每一行的第一个非零元素在前一行的第一个非零元素右边。我们看几个例子:
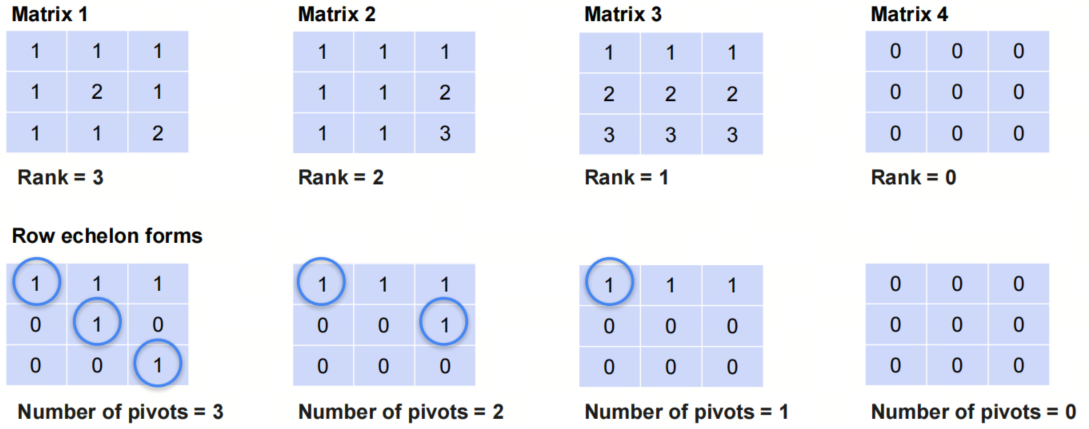
- pivot在英文中有:枢纽,轴的意思,在线性代数的语境下,翻译成‘主元’。
4.1 最简行阶梯形矩阵 Reduced Row Echelon Form
最简行阶梯形矩阵是指行阶梯形矩阵的主元为1,且主元所在列的其他元素都为0。
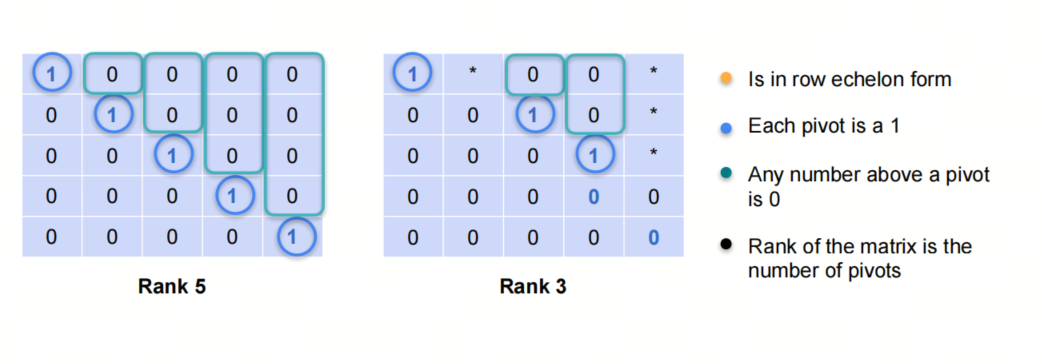
5. 高斯消元法 Gauss Elimination Algorithm
高斯消元法是一种求解线性方程组的方法,它的基本思想是通过行变换将系数矩阵化为行阶梯形矩阵,然后通过回代求解。
- 该方法以数学家高斯命名,由拉布扎比.伊丁特改进,发表于法国,但最早出现于中国古籍《九章算术》,成书于约公元前150年
增广矩阵Augmented Matrix 是指将系数矩阵和常数矩阵合并在一起的矩阵。

通过高斯消元法,我们最终会得到这样的结果:
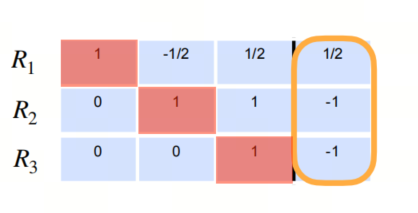
再经过回代,我们可以得到方程组的解。
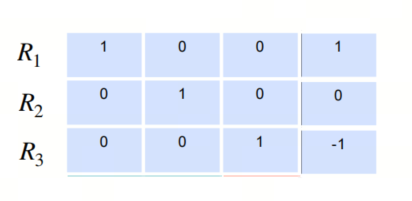
下面给出高斯消元法的python代码:
def gaussian_elimination(A, b):
n = len(A)
# Augment the matrix A with the vector b
for i in range(n):
A[i].append(b[i])
# Forward elimination
for i in range(n):
# Find the pivot
max_row = i
for k in range(i+1, n):
if abs(A[k][i]) > abs(A[max_row][i]):
max_row = k
# Swap the rows
A[i], A[max_row] = A[max_row], A[i]
# Make all rows below this one 0 in current column
for k in range(i+1, n):
c = -A[k][i] / A[i][i]
for j in range(i, n+1):
if i == j:
A[k][j] = 0
else:
A[k][j] += c * A[i][j]
# Back substitution
x = [0 for _ in range(n)]
for i in range(n-1, -1, -1):
x[i] = A[i][n] / A[i][i]
for k in range(i-1, -1, -1):
A[k][n] -= A[k][i] * x[i]
return x
# 示例使用
A = [
[2, 1, -1],
[-3, -1, 2],
[-2, 1, 2]
]
b = [8, -11, -3]
solution = gaussian_elimination(A, b)
print("解:", solution)
参考
[1] machine-learning-linear-algebra
[2] 高斯消元法
欢迎关注我的GitHub和微信公众号[真-忒修斯之船],来不及解释了,快上船!
仓库上有原始的Markdown文件,完全开源,欢迎大家Star和Fork!