LLMForEverybody
0基础学习AI大模型必备数学知识之线性代数(三)向量和线性变换
1. 系列介绍
AI是理科+工科的交叉学科,牢固的数学知识有助于理解算法的本质。
线性代数是AI领域的基础数学知识之一,掌握线性代数知识对于理解深度学习算法和模型至关重要。本系列将介绍AI大模型必备的线性代数知识,帮助大家更好地理解AI大模型的原理和应用。
我们会着重介绍各种基础概念,关键数学名词会加注英文以求更好的理解。我们也会分享一些大学里老师不会教的小知识,目的是帮助大家建立起对线性代数的直觉式认识。
2. 向量
向量是一个具有大小和方向的数学对象。它在物理学、工程学和数学中广泛应用,用于表示具有方向的量,如力、速度和位移等。向量通常用箭头表示,箭头的长度代表大小(或模),箭头的方向代表方向。
2.1 向量间的计算 Operations on Vectors
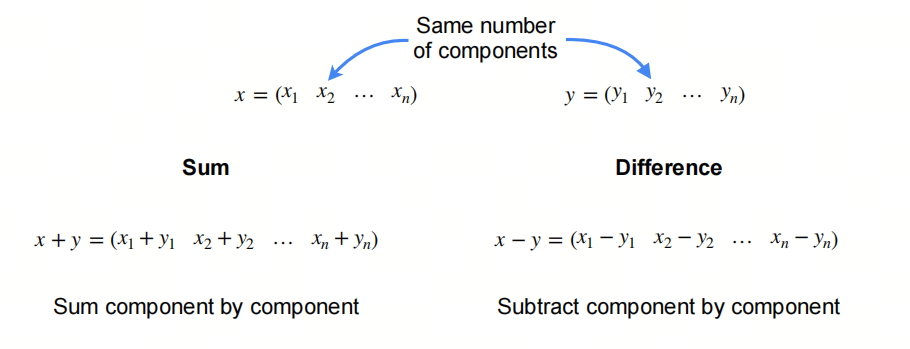
向量的加法是指将两个向量相加,得到一个新的向量。向量的加法满足交换律和结合律。
向量的减法是指将两个向量相减,得到一个新的向量。
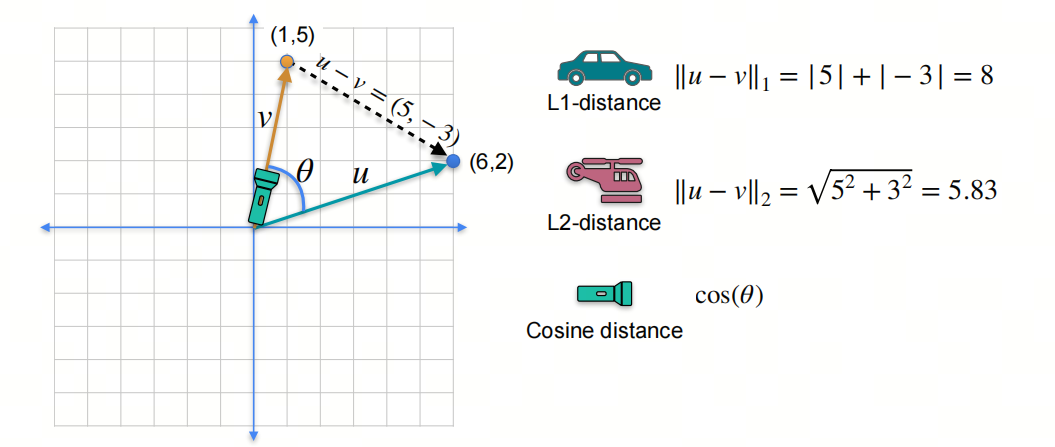
2.2 距离 Distance
L1-norm和L2-norm是两种常见的距离计算方法:
L1-norm(机器学习中又称为曼哈顿距离)是指向量中各个元素绝对值之和;
L2-norm(机器学习中又称为欧式距离)是指向量中各个元素的平方和再开方;
余弦相似度是指两个向量之间的夹角余弦值。
2.3 点积 Dot Product
点积是两个向量相乘得到的标量。点积的几何意义是两个向量之间的投影。
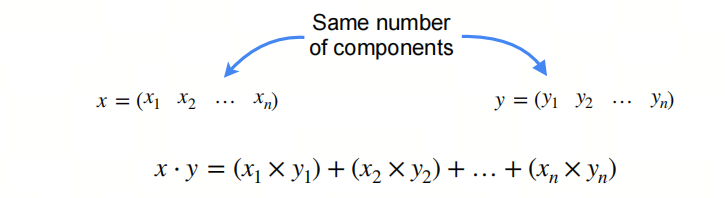
点积有两种表示方式:$x·y$ 和 $<x,y>$
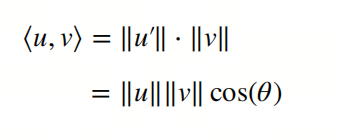
2.4 哈达玛积 Hadamad Product
两个向量元素相乘得到一个新向量的操作称为哈达玛积(Hadamard product),也称为逐元素乘积(element-wise product)或Schur积。这种操作在数学、物理学和工程学中非常常见,特别是在矩阵理论,信号处理,大模型等领域。
哈达玛积的定义如下:
给定两个维度相同的向量 $\mathbf{a} = [a_1, a_2, \ldots, a_n]$ 和 $\mathbf{b} = [b_1, b_2, \ldots, b_n]$,它们的哈达玛积是一个新向量 $\mathbf{c} = [c_1, c_2, \ldots, c_n]$,其中每个元素$c_i$ 是对应元素 $a_i$ 和 $b_i$ 的乘积,即:
$c_i = a_i \cdot b_i$
对于所有的 $i = 1, 2, \ldots, n$。
3. 线性变换 Linear Transformations
矩阵和向量相乘是一种线性变换,它将一个向量映射到另一个向量。矩阵和向量相乘的结果是一个新的向量。
3.1 秩和线性变换
假设我们有一个矩阵 \(\begin{pmatrix} 3 & 1 \\ 1 & 2 \end{pmatrix}\)
我们说它事实上是一个线性变换,因为它将一个向量映射到另一个向量。如何理解?
在我们原始的二维空间中,我们有一个向量 $\begin{pmatrix} 1 \ 1 \end{pmatrix}$,它的坐标是 $(1,1)$。当我们将这个向量乘以矩阵时,我们得到一个新的向量 $\begin{pmatrix} 5 \ 3 \end{pmatrix}$,它的坐标是 $(4,3)$。
同样的,对另外三个坐标点$(0,0)$,$(1,0)$,$(0,1)$,我们可以得到新的坐标点$(0,0)$,$(3,1)$,$(1,2)$。
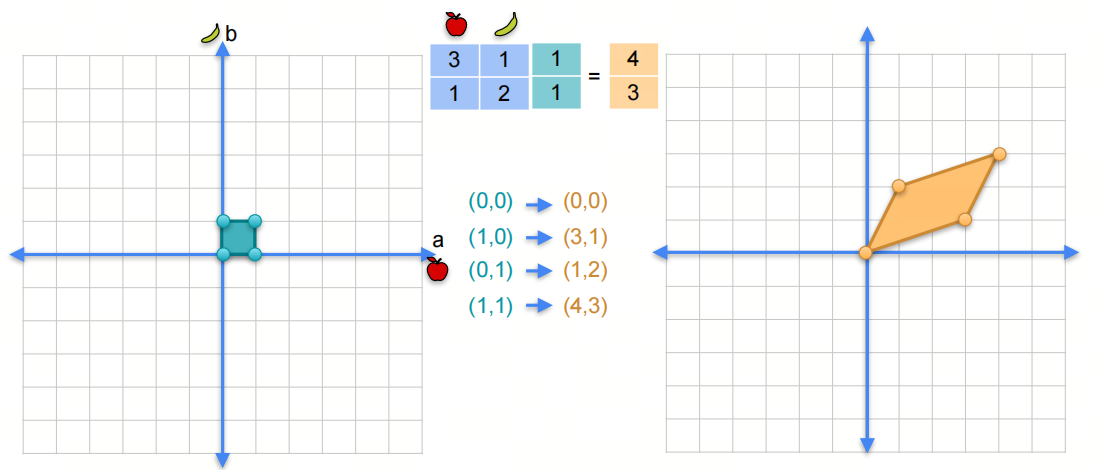
相当于把原来的坐标(系)都进行了线性变换。
- 有的小伙伴可能会注意到,新的坐标点$(0,0)$,$(3,1)$,$(1,2)$,$(4,3)$做成的平行四边形的面积正好是矩阵的秩,这是个巧合吗?
3.2 单位矩阵 The identity matrix
identity 在英语中有‘身份’的意思,在数学术语中,identity也表示恒等式。 The identity matrix表示一个矩阵和向量相乘后,得到的向量和原向量相同。
单位矩阵是一个方阵,对角线上的元素都是1,其他元素都是0。单位矩阵通常用 $I$ 表示。
3.3 逆矩阵 Inverse
一个矩阵和它的逆矩阵相乘得到单位矩阵。
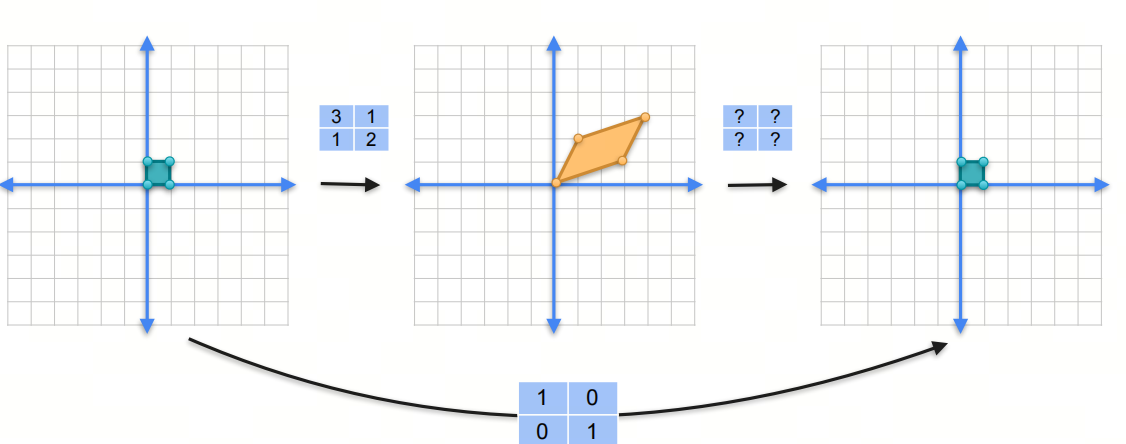
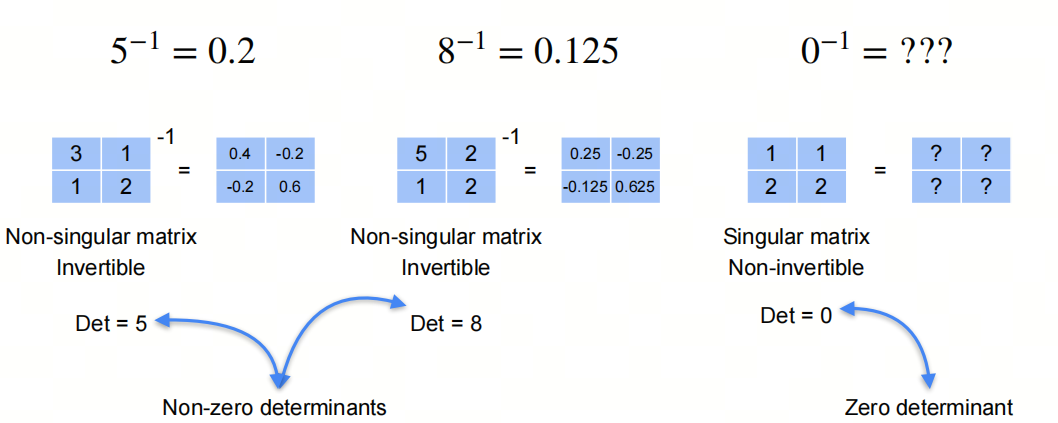
非奇异的矩阵才是可逆的,奇异矩阵是不可逆的。为什么呢?欢迎关注下一篇文章。
参考
[1] machine-learning-linear-algebra
欢迎关注我的GitHub和微信公众号[真-忒修斯之船],来不及解释了,快上船!
仓库上有原始的Markdown文件,完全开源,欢迎大家Star和Fork!