LLMForEverybody
0基础学习AI大模型必备数学知识之线性代数(一)矩阵,奇异性和行列式
1. 系列介绍
AI是理科+工科的交叉学科,牢固的数学知识有助于理解算法的本质。
线性代数是AI领域的基础数学知识之一,掌握线性代数知识对于理解深度学习算法和模型至关重要。本系列将介绍AI大模型必备的线性代数知识,帮助大家更好地理解AI大模型的原理和应用。
我们会着重介绍各种基础概念,关键数学名词会加注英文以求更好的理解。我们也会分享一些大学里老师不会教的小知识,目的是帮助大家建立起对线性代数的直觉式认识。
2. 矩阵 matrix
对于我来说,第一次听到‘Matrix’ 这个词还是来源于《黑客帝国》(《The Matrix》)这部电影。在电影中,Matrix是一个虚拟世界,是由机器人控制的,人类被困在这个虚拟世界中,而不知道真实的世界是什么样子。
首先,矩阵只是matrix的一个翻译,matrix一词来自拉丁语,表示 “子宫”之意,子宫是孩子诞生之处,故也引申为各种事物的源出之处,即“发源地”。这个词后来被用在各种学科中。
在数学中,用其表示按照长方阵列排列的复数或实数集合,书写时用外括号括起来。方阵中设置不同的数字,从而生成不同阵列参数,这阵列参数及其理论广泛应用于电路学、力学、光学、量子物理学、计算机运算中。西尔维斯特将之命名为matrix,中文翻译为“矩阵”。从另外一个角度看,矩阵外括号包围着内部数据,形态上也像子宫孕育着即将诞生的婴儿一般。
- 我在先前的文章中将矩形排布的序列称为“Matrix”,盖因从中可以产生出各种不同的行列式,就如由同一个母体的子宫中孕育出来一样 —- 西尔维斯特
3. 奇异性 singularity
singular 作为形容词在英文中有两个意思:1. 单数的,2. 特别的;引人注意的. 在线性代数的语境中,我们取第二个意思,即特别的,引人注意的。并翻译成固定的数学名词 奇异 / 奇异的;
为此 singularity作为名词,翻译成 奇异性 / 奇异点;
有 奇异的, 那肯定有 非奇异的,即 non-singular。
那什么样的矩阵是 奇异的呢?换言之,什么样的矩阵是 引人注意的 呢?
我们用几个句子来类比一下:
3.1 句子类比1

上面有三组句子对,每组有两个句子:
- 第一组句子描述有一只黑狗和一只橘猫,我们说这样的句子组是 完备的( complete);
- 第二组句子描述有一只黑狗和一只黑狗,我们说这样的句子组是 冗余的( redundant);
- 第三组句子描述有一只黑狗和一只白狗,我们说这样的句子组是 矛盾的( contradictory)。
完备的句子组是非奇异的,冗余和矛盾的句子组是奇异的,这和现实生活中的逻辑是一样的,好事不出门,坏事传千里。不好的东西总是引人注意的。
3.2 句子类比2
对于更多的句子组,可以类比上述的方式看出其奇异性。
3.3 数学思考
完备的线性方程组有唯一解,冗余的线性方程组有无穷多解,矛盾的线性方程组没有解。这和上面的句子类比是一样的。
4. 行列式 determinant
对于一个矩阵,我如何判断它是奇异的还是非奇异的呢?这就要用到行列式的概念。
determinant 在英文中的意思是:决定因素。在线性代数的语境中,determinant决定了一个矩阵是奇异的还是非奇异的。也就是矩阵对应的增广矩阵(augmented matrix)是否有解和解的唯一性。我们将其翻译成 行列式。
-
如果你不知道什么是增广矩阵,不用担心,我们会在下一篇文章中介绍。
-
关于行列式一词的由来: 矩阵 之前被称为 行列,那决定 行列奇异性的计算公式值determinant,就是 行列式了,后来,行列改名为 矩阵,但 行列式 这个名字却一直保留了下来。
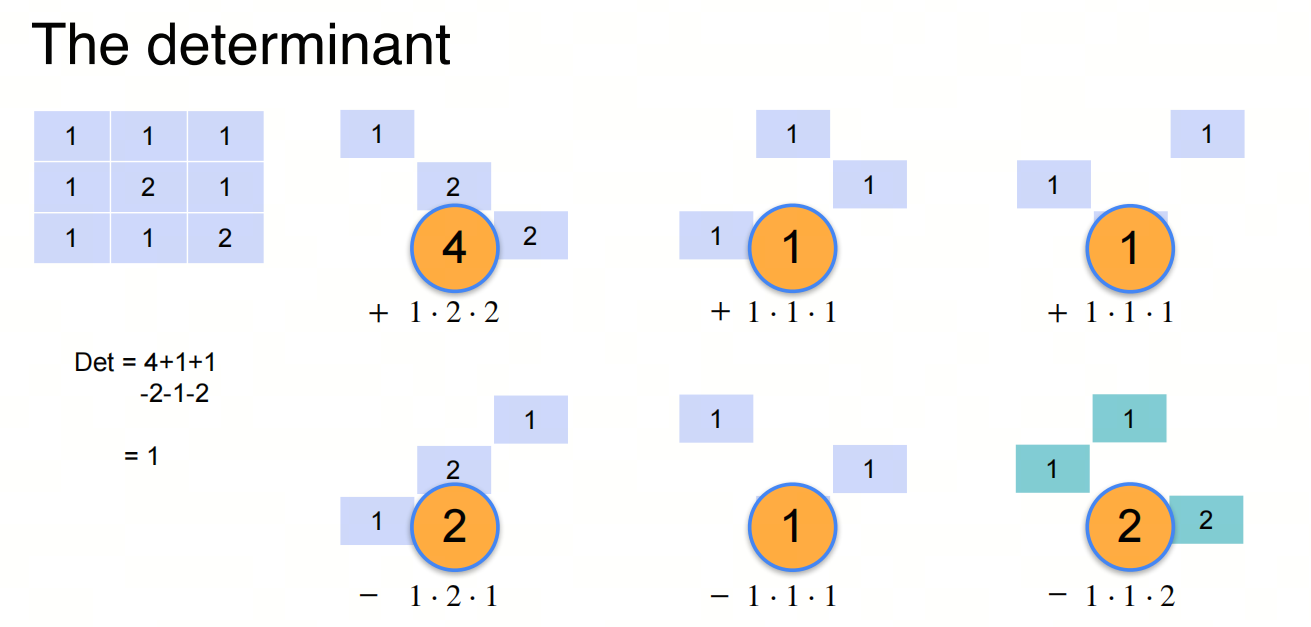
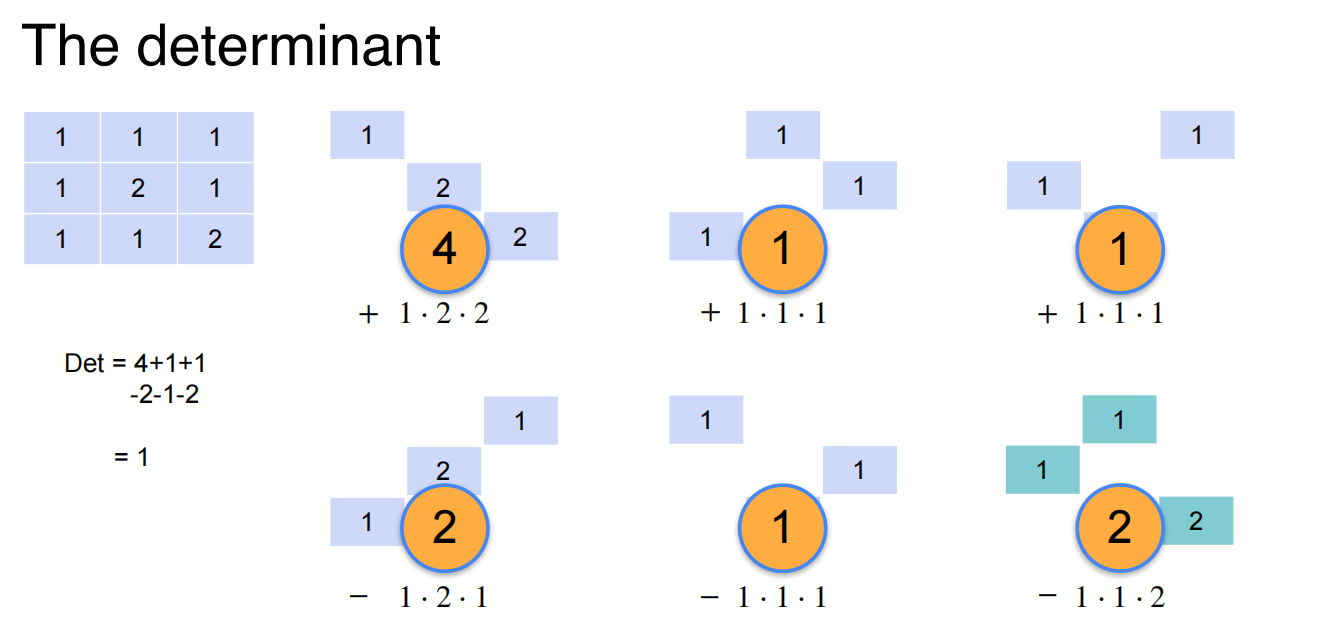
4.1. 行列式的计算
一个 $n$ 阶方块矩阵 $A$ 的行列式可直观地定义如下:
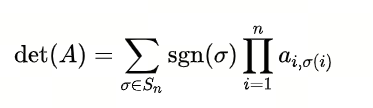
其中 $S_{n}$ 是集合 ${ 1,2,…,n }$上置换的全体,即集合 ${1,2,…,n}$ 到自身上的一一映射(双射)的全体.
除非你想要继续深入学习线性代数,否则你不需要知道上述的定义。我们只需要知道行列式的直观计算逻辑即可。
参考
[1] machine-learning-linear-algebra
[2] Matrix和《黑客帝国》
[3] wiki:矩阵
[4] wiki:西尔维斯特
欢迎关注我的GitHub和微信公众号[真-忒修斯之船],来不及解释了,快上船!
仓库上有原始的Markdown文件,完全开源,欢迎大家Star和Fork!