LLMForEverybody
每天3分钟,彻底弄懂神经网络的优化器(二)SGD
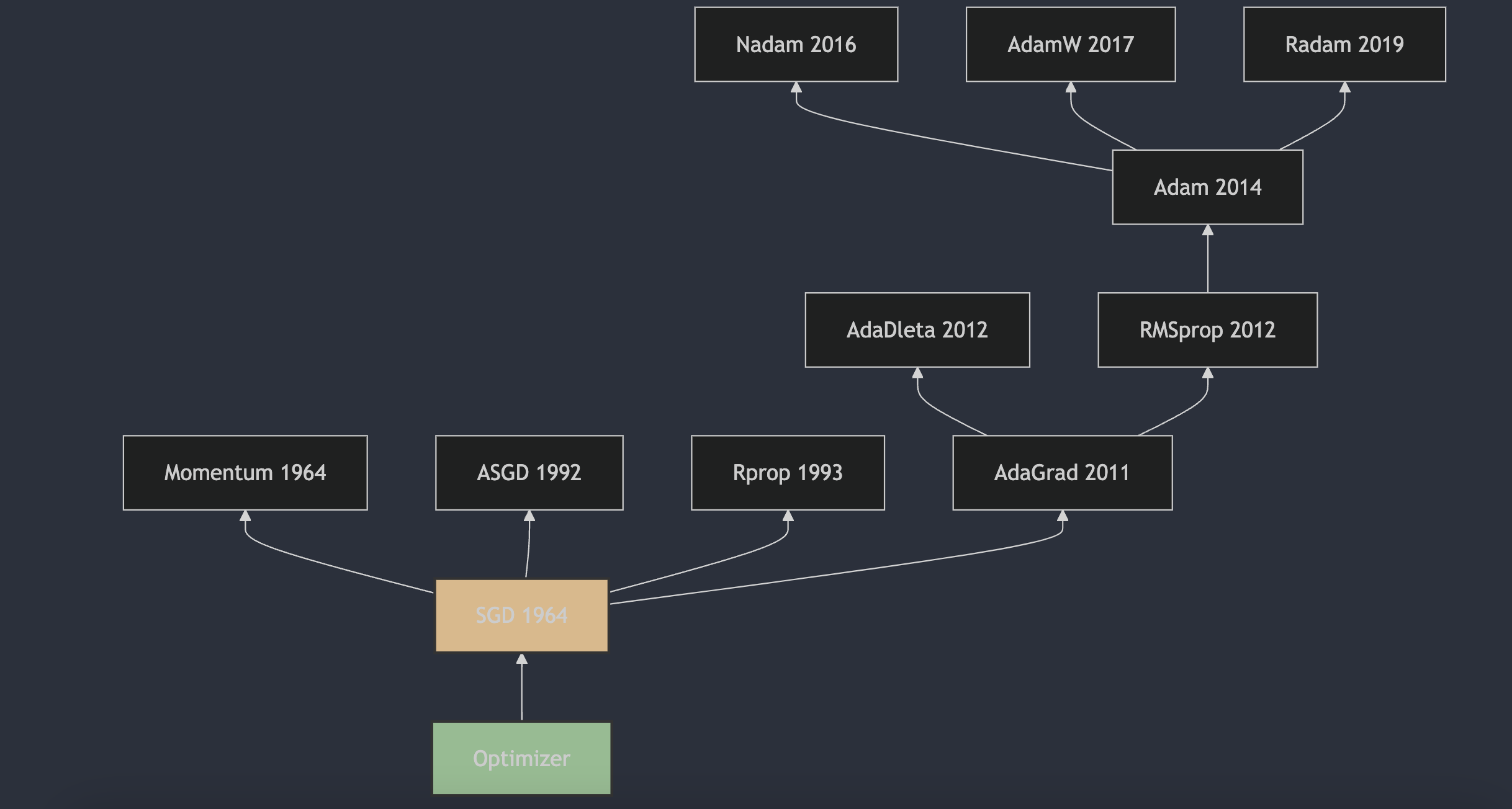
1. SGD
随机梯度下降(Stochastic Gradient Descent,SGD)是一种用于优化可微分目标函数的迭代方法,它是梯度下降优化的随机近似。SGD的提出可以追溯到1951年,由Herbert Robbins和Sutton Monro在他们的论文《A Stochastic Approximation Method》[1]中首次描述了随机近似方法,这可以看作是SGD的前身。随后,J. Kiefer和J. Wolfowitz在1952年发表了论文《Stochastic Estimation of the Maximum of a Regression Function》[2],这篇论文更接近于机器学习领域中SGD的现代理解。
随机梯度下降(SGD)的更新公式是梯度下降法的一种变体,它用于优化目标函数,特别是在处理大规模数据集时。SGD 在每次迭代中只使用一个或一小批样本来计算梯度,然后更新模型参数。这样做可以减少每次迭代的计算成本,并有助于算法逃离局部最小值。
SGD 的参数更新公式如下:
\[\theta_{t+1} = \theta_t - \eta_t \nabla J(\theta_t; x^{(i)}, y^{(i)})\]其中:
- $\theta_t$表示在时间步 t的模型参数(可以是权重和偏置);
- $\eta_t$表示学习率,用于控制参数更新的步长;
- $\nabla J(\theta_t; x^{(i)}, y^{(i)})$表示损失函数 J 对参数 $\theta_t$ 在样本 $(x^{(i)}, y^{(i)})$ 处的梯度;
- $\theta_{t+1}$是更新后的模型参数。
在实际应用中,学习率$\eta_t$可以是一个固定的值,也可以随着时间步逐渐减小(学习率衰减),以确保算法在训练过程中的稳定性和收敛性。
2. SGD的缺点-非凸优化问题
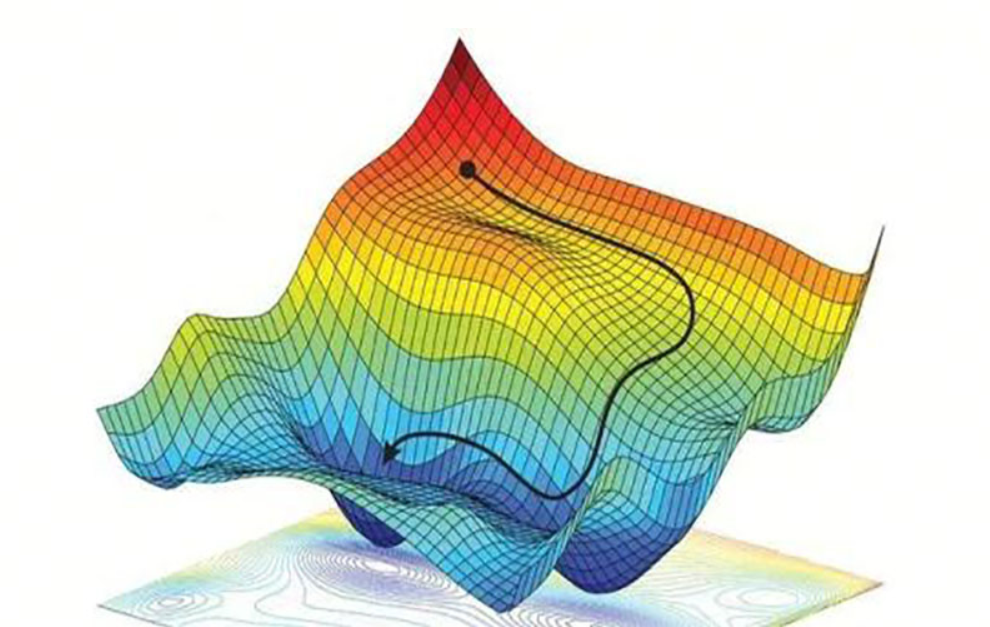
非凸优化问题是指目标函数具有多个局部最小值的情况,这种情况下,SGD可能会陷入局部最小值,并且很难跳出。这是因为SGD在每次迭代中只使用一个或一小批样本来计算梯度,这样可能导致梯度的方向不准确,从而影响参数更新的方向。
鞍点
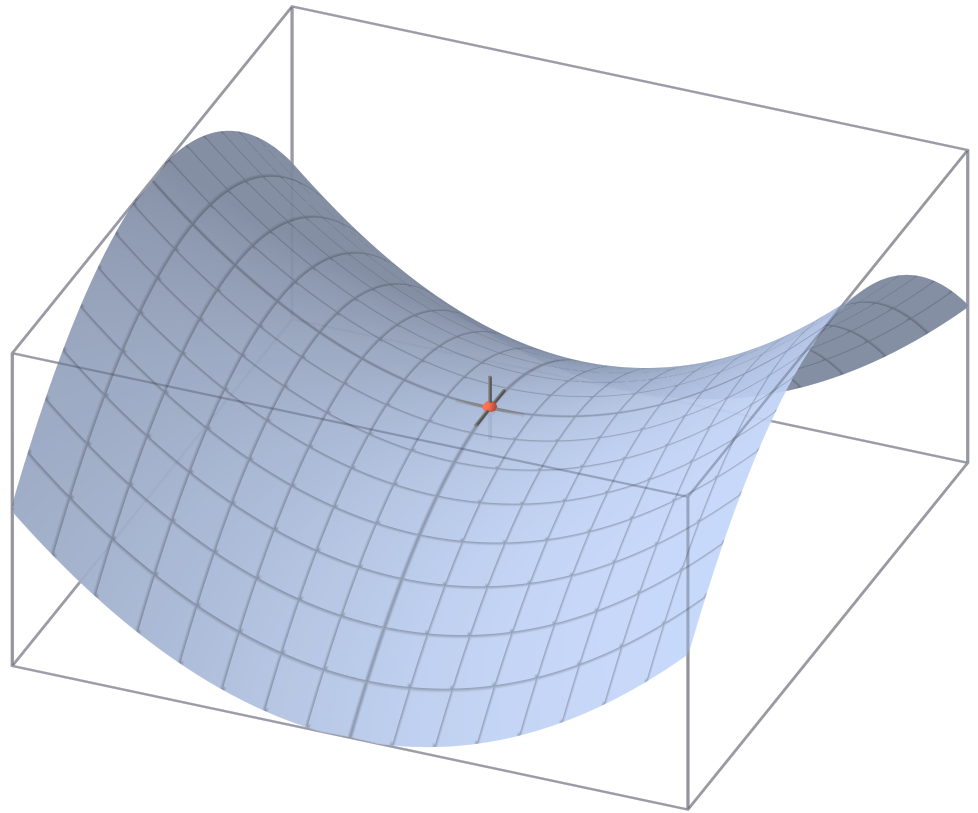
在优化和机器学习领域,鞍点(Saddle Point)是指目标函数的临界点,在这个点上,某些方向的导数为正(上升),而另一些方向的导数为负(下降)。换句话说,鞍点既不是局部最小值也不是局部最大值,而是局部最小值和局部最大值的某种组合。
具体来说:
- 局部最小值:在该点的所有邻域内,函数值都大于或等于该点的函数值;
- 局部最大值:在该点的所有邻域内,函数值都小于或等于该点的函数值;
- 鞍点:在该点的某些邻域方向上,函数值大于或等于该点的函数值,而在另一些邻域方向上,函数值小于或等于该点的函数值。
在二维空间中,可以将鞍点想象成马鞍的形状,从马鞍的一侧走到顶部再走到另一侧,你会先经历一个上升过程(局部最小值的特征),然后是一个下降过程(局部最大值的特征)。
在机器学习中,尤其是在深度学习中,鞍点的存在可能会使基于梯度的优化算法(如梯度下降)遇到难题,因为梯度下降算法可能会在接近鞍点时停滞不前,因为梯度在该点为零,算法无法判断下一步应该向哪个方向移动。
参考
[1] A Stochastic Approximation Method
[2] Stochastic Estimation of the Maximum of a Regression Function
欢迎关注我的GitHub和微信公众号,来不及解释了,快上船!
仓库上有原始的Markdown文件,完全开源,欢迎大家Star和Fork!