LLMForEverybody
多年以后,面对FlashAttention,你会忍不住想起高三上学期的那节数学课。那时,暑假刚刚结束,烈日当空,教室里就像蒸笼一样,连空气都懒得流动。阳光透过窗帘的缝隙,像个顽皮的小孩,时不时跳到黑板上,给老师的公式镀上一层金边。老师在黑板前唾沫横飞,激情四溢地讲述着什么“等比数列”和“极限”,而你的脑袋却飞到了食堂,幻想着中午能不能抢到那份热气腾腾的番茄炒蛋。
“看好了,我要变形了!”老师的声音突然拔高,仿佛他要变身成超人。你这才从对食堂美食的遐想中惊醒,心想:变形?这数学题能变成午餐吗?教室里的同学们也都在努力保持清醒,有的趴在桌子上如同死去的昆虫,有的则在心里默默计算着这节课还剩多少时间。阳光在教室里肆意挥洒,照得你恍惚间觉得,或许数学也能像食堂的饭菜一样,变得简单易懂。
1 FlashAttention
Flash Attention 是一种新型的注意力机制算法,由斯坦福大学和纽约州立大学布法罗分校的科研团队共同开发,旨在解决传统 Transformer 模型在处理长序列数据时面临的时间和内存复杂度高的问题。该算法的核心思想是减少 GPU 高带宽内存(HBM)和 GPU 片上 SRAM 之间的内存读写次数,通过分块计算(tiling)和重计算(recomputation)技术,显著降低了对 HBM 的访问频率,从而提升了运行速度并减少了内存使用。
Flash Attention 通过 IO 感知的设计理念,优化了内存访问模式,使得 Transformer 模型在长序列处理上更加高效,为构建更长上下文的高质量模型提供了可能。
2 大模型需要的显卡知识
我们需要明确大模型训练与推理的基本需求。大模型通常意味着更高的计算需求和数据存储需求。因此,在选择GPU时,我们需要关注其计算能力、显存大小以及与其他硬件设备的兼容性。
计算墙,指的是单卡算力和模型总算力之间的巨大差异。A100 的单卡算力只有 312 TFLOPS,而 GPT-3 则需要 314 ZFLOPs 的总算力,两者相差了 9 个数量级。
显存墙,指的是单卡无法完整存储一个大模型的参数。GPT-3 的 1750 亿参数本身就需要 700 GB 的显存空间(每个参数按照 4 个字节计算),而 NVIDIA A100 GPU 只有 80 GB 显存。
通信墙,主要是分布式训练下集群各计算单元需要频繁参数同步,通信性能将影响整体计算速度。如果通信墙如果处理得不好,很可能导致集群规模越大,训练效率反而会降低。
当前显卡的计算能力是大于通信能力的,使得通信成为瓶颈,transformer的self-attention,会有大量的IO,即将数据从HBM读取到SRAM中再计算。
为此,FlashAttention的设计理念是通过增加计算量的方式减少I/O,来平衡当前显卡计算能力强于通信能力的特点。
Self-Attention
为了看懂FlashAttention的核心算法,让我们从原始的Self-Attention开始。参考From Online Softmax to FlashAttention1
Self-Attention的计算,去掉batch和缩放因子,可以概括为:
$Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$
其中,Q,K,V,O都是2维矩阵,形状是(L, D), L是序列长度,D是每个头的维度,softmax函数作用在后面的维度上。
标准的计算self-attention的计算流程有三步:
对于FlashAttention,我们不需要将X,A放到全局内存(HBM)上;我们将(1)放在一个cuda-kernel/tensor-kernel上。这样,我们就不需要大量的I/O。
FlashAttention不需要在全局内存上实现 X 和 A 矩阵,而是将公式(1)中的整个计算融合到单个 CUDA 内核中。这要求我们设计一种算法来仔细管理片上内存(on-chip memory)(如流算法),因为 NVIDIA GPU 的共享内存(SRAM)很小。对于矩阵乘法等经典算法,使用平铺(tiling)来确保片上内存不超过硬件限制。这种平铺方法是有效的原因是:加法是关联的,允许将整个矩阵乘法分解为许多平铺矩阵乘法的总和。然而,Self-Attention 包含一个不直接关联的 softmax 运算符,因此很难简单地平铺 Self-Attention。有没有办法让 softmax 具有关联性?
Gut-feeling:我们的目标是计算O,一般来说,我们需要获取所有的Q,K,V,然后分三步计算;我们也可以先获取一小块Q,K,V,一次计算得到部分的O,再想办法将部分的O合成全部的O。
难点:矩阵是可加的,但是soft-max是不可加的。
解决方案:高考数学最后一题–等比数列
Safe Softmax
对于softmax,公式如下:
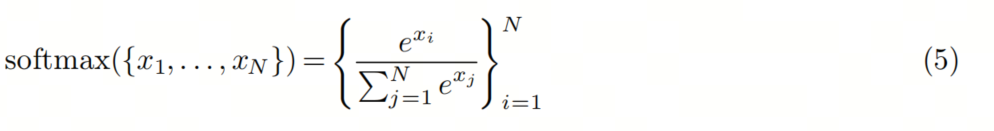
x_i 可能会非常大,那e^x_i会溢出:float16最大65536,那x_i大于12时,e^x就超过有效数字了。所以事实上的公式是safe-softmax:

其中:
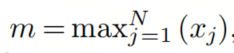
基于此,我们可以总结下safe-softmax的计算步骤,称之为3步算法

这就是传统的self-attention算法,需要我们从1到N迭代3次。{x_i}是由QK计算出来的pre-softmax,这意味着我们需要读取Q,K三次,有很大的I/O开销。
Online Softmax
如果我们在一个循环中融合方程 7、8 和 9,我们可以将全局内存访问时间从 3 减少到 1。不幸的是,我们不能在同一个循环中融合方程 7 和 8,因为 8 取决于 m_N,而 m_N 只有在第一个循环完成之后才能确定。
注意:高考数学来了!
为了移除对N的依赖,我们可以创建另一个序列作为原始序列的替代。即找到一个等比数列(递归形式),去除N的依赖。
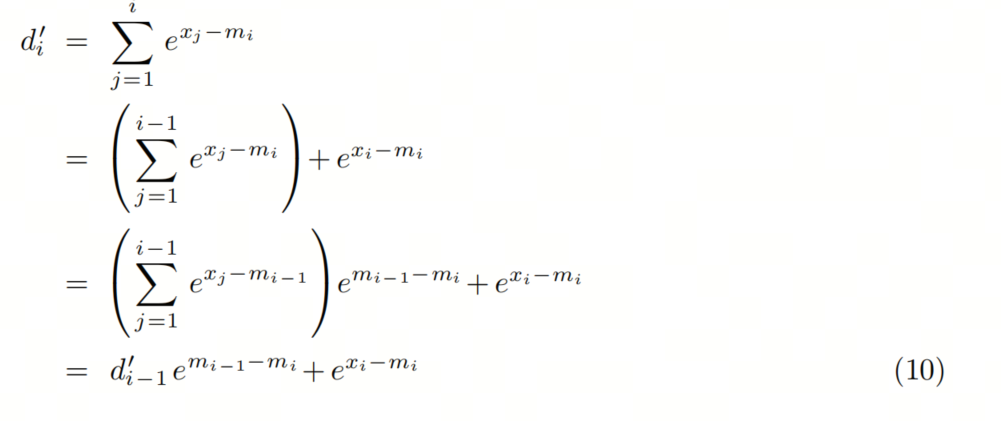
这个递归形式只依赖于m_i 和 m_i-1,我们可以在同一个循环中同时计算 m_j 和 d’_j.

这是 Online Softmax 论文中提出的算法。但是,它仍然需要两次传递才能完成 softmax 计算,我们能否将传递次数减少到 1 次以最小化全局 I/O?
FlashAttention
不幸的是,对于 softmax 来说,答案是不行,但在 Self-Attention 中,我们的最终目标不是注意力得分矩阵 A,而是等于 A V 的 O 矩阵。我们能找到 O 的一次递归形式吗?将 Self-Attention 计算的第 k 行(所有行的计算都是独立的,为了简单起见,我们只解释一行的计算)公式化为递归算法:

我们将公式 12 中的 a_i替换为公式 11 中的定义:

这仍然取决于 m_N 和 d_N,这两个值在前一个循环完成之前无法确定。但我们可以再次使用Online softmax节中的替代技巧,即创建替代序列 o’
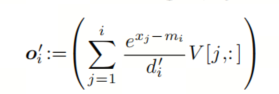
我们可以找到 o_i 和 o_i-1 之间的递归关系
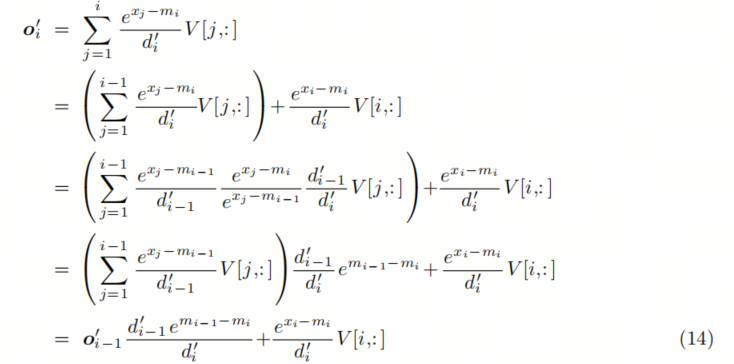
我们可以将 Self-Attention 中的所有计算融合到一个loop中:
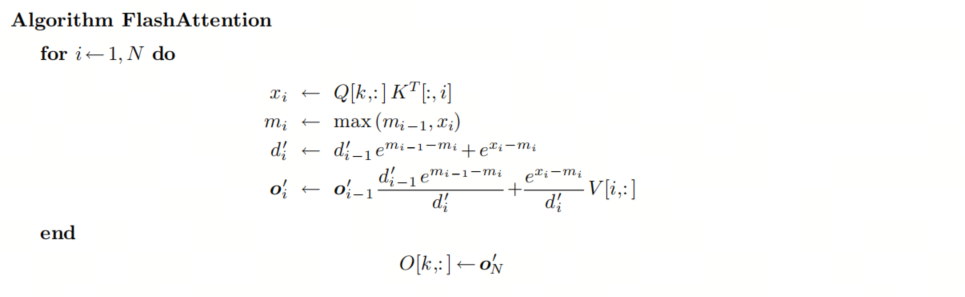
此时,所有的数据都非常小并且可以加载到GPU的SRAM里面,由于该算法中的所有操作都是关联的,因此它与平铺兼容。如果我们逐个平铺地计算状态,则该算法可以表示如下:

总结
FlashAttention最核心的部分是构造出一个递归(等比数列),让部分结果可以累计到全局,这样就不用一下子加载所有值并分步计算了。
这个等比数列的构造,大概就是高考最后一道大题的水平。
参考
[1] From Online Softmax to FlashAttention: https://courses.cs.washington.edu/courses/cse599m/23sp/notes/flashattn.pdf