LLMForEverybody
从欧拉公式的美到旋转位置编码RoPE
也许你在某些场合听说过欧拉公式,也许你干脆对数学不感冒。机缘巧合下,你点开了这篇文章,大致浏览了下然后关闭,继续为自己的工作学习忙碌。这不妨碍你暂停忙碌的脚步,欣赏她的美。 若干年后,你应该不曾记得看过这篇文章,但你会记得数学界有一个很美的公式。
1. 欧拉公式和欧拉恒等式
欧拉公式(Euler’s formula)是复分析领域的公式,它将三角函数与复指数函数关联起来,因其提出者莱昂哈德·欧拉而得名。欧拉公式提出,对任意实数 x,都存在: \(e^{ix} = \cos(x) + i\sin(x)\) 其中 e是自然对数的底数,i是虚数单位,而 cos和 sin则是余弦、正弦对应的三角函数,参数 x则以弧度为单位。
这是一个非常美丽的公式,它将三角函数,指数函数,复数联系在了一起,是数学中的一颗明珠。
欧拉恒等式(Euler’s identity)是欧拉公式的一个特例,当 x = π 时,欧拉公式变为: \(e^{i\pi} + 1 = 0\) 这个公式被认为是数学中最美丽的公式之一,它将五个最重要的数学常数联系在了一起:0、1、e、i和π。
非常感谢苏剑林大神将这么漂亮公式引入到了位置编码的设计中,大家可以关注他的博客《科学空间》https://kexue.fm/, 可以学到很多东西。
2. 预备知识
为了看懂RoPE,我们需要了解一些预备知识,包括: 1)欧拉公式 2)复数/复平面 3)三角函数的几个公式
重要!!! 在你深入大量公式之前,先要了解:
- 复平面和欧拉公式的引入,只是为了简化计算过程;
- 欧拉公式经常在数学、物理和工程领域被如此广泛应用;
- 整个证明过程,先考虑词向量为二维,再利用矩阵的特性轻松拓展到多维;
- 在证明二维场景的时候,引入复平面,原因是可以这样可以使用欧拉公式获取漂亮的数学特性,来简化过程。
3. 旋转位置编码RoPE
Rotation Position Encoding
RoPE提出为了能利用上 token 之间的相对位置信息,假定 query 向量$q_m$ 和 key 向量 $k_n$之间的内积操作可以被一个函数$g$表示,该函数$g$的输入是词嵌入向量$x_m$,$x_n$ 和它们之间的相对位置$m-n$:
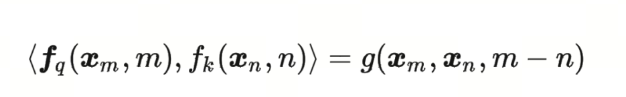
大胆假设,小心求证。 现在我们的目标就是找到一个合适的函数$g$,使得$g(x_m, x_n, m-n)$能够捕捉到词向量之间的相对位置信息。
RoPE提出,在词向量是二维的情况下,将平面转化为复平面,如果我们按照如下的方式定义函数$f$,则可以找到对应的$g$
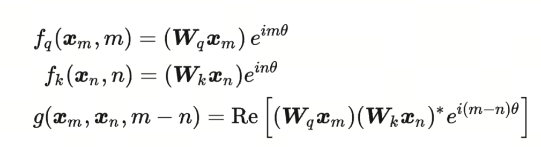
$Re$指的是复数的实数部分,更近一步,我们可以将函数$f$定义为:
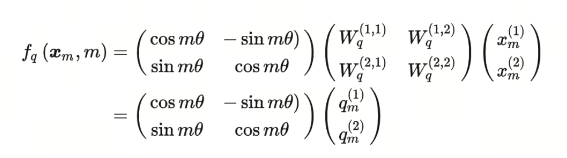
这边,不就是原来的query矩阵乘上了一个旋转矩阵吗?也就是说,加上$m$这个位置信息后,如果使用RoPE的设计方案,就相当于将原query矩阵进行了旋转。这就是旋转的由来。
同理,$f_K$可以表示为:
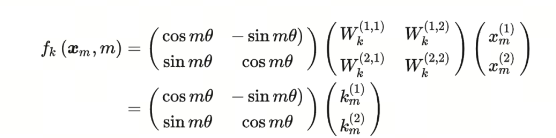
那么,对应的$g$函数就是:
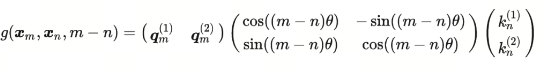
4. 从二维到多维
在二维场景下,我们引入了复平面,是为了使用欧拉公式获取漂亮的数学特性,来简化过程。但是在多维场景下,我们可以直接使用矩阵的特性,来简化过程。将2维的RoPE推广到多维的RoPE,只需要将2维的RoPE的旋转矩阵$R$替换为多维的旋转矩阵$R$即可。
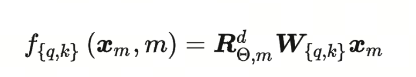
因为内积满足线性叠加性质,所以任意偶数维的RoPE都可以表示为二维情形拼接而成的形式。

即是在原来的$q*k$矩阵的基础上,加上了一个旋转矩阵$R^d_{\theta,m}$,这就是RoPE的设计思路。
在原始paper中,有一个直观的图
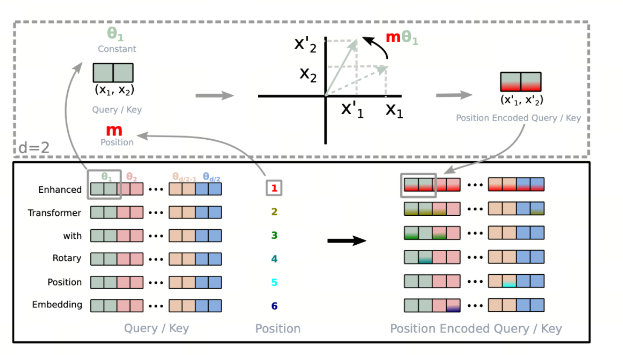
5.RoPE的证明
注意,现在的证明是建立在二维的基础上,二维可以用上一节的矩阵特性推广到多维。 二维的情况下,形式上我们将其转化为复平面。
按照RoPE的设计,编码后的$q,v$和内积$<q,v>$的形式是:
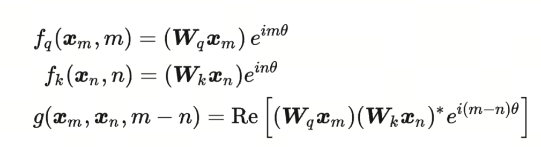
为什么上述公式满足:
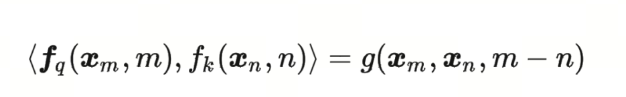
首先,我们看到欧拉公式 \(e^{ix} = \cos(x) + i\sin(x)\) 则有:
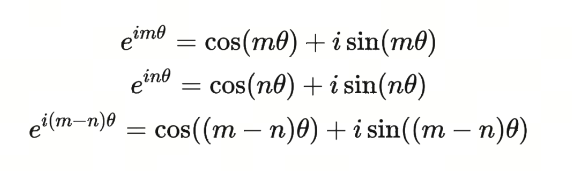
我们看query矩阵,可以看到:
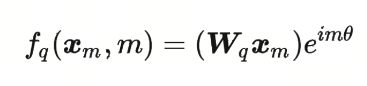
其中$W_q$是二维矩阵,$x_m$是二维向量,其乘积是一个二维向量,这边我们用$q_m$表示。$q^{(1)}_m$,$q^{(2)}_m$分别表示第一维和第二维。
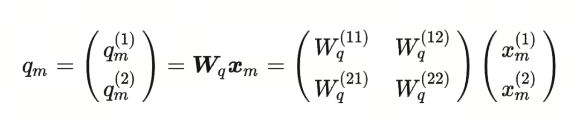
我们这时,需要将$q_m$转化为复数形式,即将这个二维平面放到复平面上,复平面的实部是第一维(x轴),虚部是第二维(y轴)。
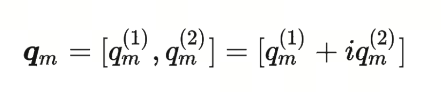
这时,我们可以将$f_q(x_m,m)$表示为:
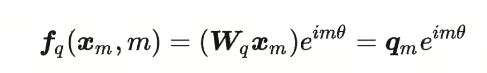
这就是两个复数的积(将复数带入)
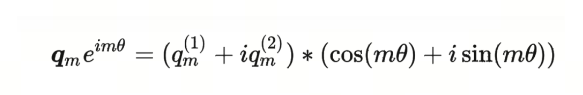
经过简单的展开:
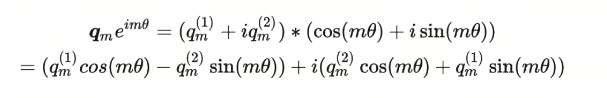
再重新从复平面回到实数二维平面,我们可以将上述公式表示为:
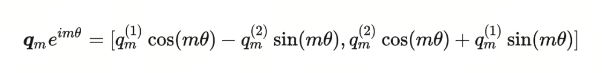
事实上这就是没有位置信息的query向量乘上了一个旋转矩阵,这就是RoPE的设计思路。
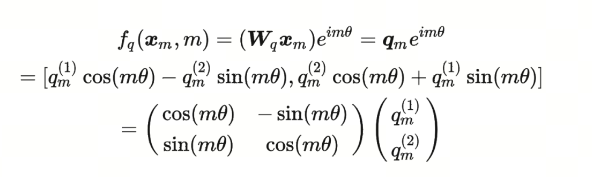
同理,我们可以得到key向量的RoPE形式:
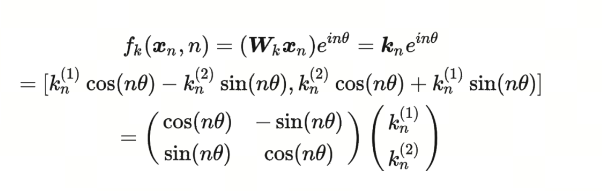
最后,我们可以得到RoPE的内积形式:
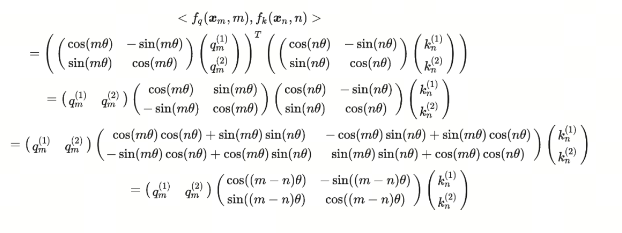
总结
RoPE非常巧妙的借助复平面和欧拉公式,将位置信息编码到了query和key向量中,使得模型能够利用上token之间的相对位置信息。RoPE的设计思路是将query和key向量进行旋转,这就是旋转的由来。
参考
[1] 十分钟读懂旋转编码(RoPE)
[3] Transformer升级之路:2、博采众长的旋转式位置编码
[4] Transformer学习笔记一:Positional Encoding(位置编码)
[5] RoFormer: Enhanced Transformer with Rotary Position Embedding